- Question
If a, b and c are positive integers such that ab = 432 bc = 96 and c < 9, then the smallest possible value of a + b + cis:
a)59
b)38
c)49
d)56
e)46
Explanation
SOLUTION[E]-
bc = 96
c < 9
Possible factors can be 48*2,32*3,24*4, 16 * 6 ,12*8
ab = 432
Possible factors can be (closest observation 9 * 48 ,18*24
From the above
a = 18
b = 24
c = 4
So, a + b + c = 46
.. The smallest value can be 46
Question-2
A, B and C have a few coins with them. 7 times the number of coins that A has is equal to 5 times the number of coins B has while 6 times the number of coins B has is equal to 11 times the number of coins C has.
What is the minimum number of coins that A, B and C put together have with them?
a)112
b)174
c)154
d)164
e)110
Explanation
SOLUTION[B]
The minimum number of coins with A, B, and C put together would be 174.
Step-by-step explanation:
Let the number of coins A, B, and C have
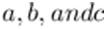
respectively.
- Then, Seven times a = Five times b
7a = 5b
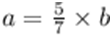
- Now, Six times b = Eleven times c
6b = 11c
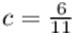
- Now, the total number of coins = a+b+c
Substituting the values of a and c from above, we obtain
- The total number of coins
- Thus, if b has 77 coins, then the total number of coins would become 174
Question-3
Determine, as to how many distinct positive integer-valued solutions exist to the equation:
(x ^ 2 – 7x + 11)(x ^ 2 – 13x + 42) = 1
a)0
b)6
c)4
d)2
e)8
Explanation
SOLUTION-[B]-6
Question-4
Mathematician, Dr. Arnav has devised a magic 3 * 3 square box, shown below, where in the sum of each row, column and diagonal is the same number, W. The entries in each of the 9 cells are given by x, y, z. Find the value of W.

a)18
b)48
c)12
d)24
e)36
Explanation
SOLUTION[E]
Question-5
If given that:
i. – y ^ 2 + x ^ 2 = 20
ii. – y ^ 3 – 2x ^ 2 – 4z >= – 12/8
iii. x, y, and z are all positive integers
Find the value of z ?
a)6
b)1
c)24
d)3
e)12
Explanation
SOLUTION[B]-1
Since x ^ 2 – y ^ 2 = 20 and x, y, z are positive integers,
(x+y)^ * (x – y) = 20 , Hence x – y, x + y are factors of 20.
Since x, y are positive integers, x+y is always positive, and for the product of (x+y)^ * (x – y) to be positiv x-y must be positive.
x, y are positive integers and x-y is positive x must be greater than y.
The possible cases are: (x + y = 10, x – y = 2) (x + y = 5, x – y = 4)
The second case fails because we get x = 9/2 y = 1/2 but x, y are integral values
For case one x = 6 y = 4 y ^ 3 – 2x ^ 2 – 4z >= – 12 Substituting the values of x and y, we have: 64 – 72 -4^ * z>-12 -8-4^ * z >= – 12
z < 1
Since x, y, z are positive integers, the only possible value for z is 1.

