Question- 1
Let x, y, z be three positive real numbers in a geometric progression such that x < y < z.
If 5x, 16y, and 12z are in an Arithmetic Progression, then the common ratio of the geometric progression shall be
a)5/2
b)1/2
c)3/5
d)1/6
e)2/5
Explanation
SOLUTION[A]-
As, x, y and z are in geometric progress
y / x = z / y = r
z / (xr) = r
z / x = r ^ 2 .
Then,
5x, 16y and 12z are in arithmetic progr
16y – 5x = 12z – 16y
32y = 5x + 12z
5x – 32y + 12z = 0
Divide by x,
5 – 32y / x + 12z / x = 0
12r ^ 2 – 32r + 5 = 0
12r ^ 2 – 30r – 2r + 5 = 0
6r(2r – 5) – (2r – 5) = 0
(6r – 1)(2r – 5) = 0
r = 1/6 or r = 5/2
But, x < y < z
1 < y / x < z / x = 1 < r < r ^ 2
ove condition is holds true for r = 5/2 only, so r = 5/2
Common ratio of geometric progression is 5/2
Question-2
A man standing on top of a tower sees a car coming towards the tower. If it takes 20 minutes for the angle of depression to change from 30° to 60°, what is the time remaining for the car to reach the tower ?
a)12 minutes
b)5 min
c)10sqrt(3) min
d)20sqrt(3) min
e)10 min
Explanation
SOLUTION[E]- Given:
It takes 20 minutes for the angle of depression to change from 30° to 60°.
Concept Used:
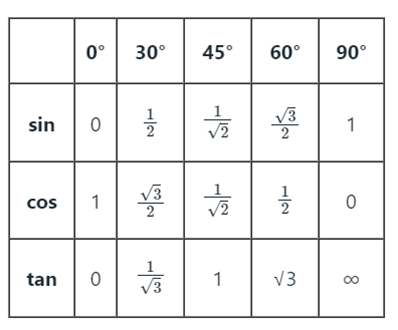
Values of Trigonometric Ratios for Common Angles:
Let AB be the tower and C1, C2 be the positions of the car
In ∆ABC1, AB = BC₁ tan 30 deg = (B*C_{2} + C_{2}*C_{1}) * 1/(sqrt(3))
Also, in ∆ABC2, AB = BC2 tan 60 deg = sqrt(3) * B*C_{2}
From (1) and (2), we get:
3B*C_{2} = B*C_{2} + C_{2}*C_{1}
C_{2}*C_{1} = 2B*C_{2}
C_{2}*C_{1} / B * C_{2} = 2/1
So, if the car takes 20 minutes to cover C₂C₁, it will take 10 minutes to cover BC2

