BODMAS, you use this phrase to decide what order to do mathematical operations in: Brackets first (from inside to outside), then Exponents, then Multiplication and Division (left to right), then Addition and Subtraction (also left to right).
BODMAS isn’t terribly fancy stuff. It’s just a useful little tool that helps us communicate clearly—it’s what tells us, for instance, that “2x(3+4)” means something different from “2×3 + 4.” But there is little something taught about what operations to do when the sum gets complicated.
BODMAS and Negative Numbers
Here’s an expression : -2^4. It looks simple, but there’s one small problem: there’s no “N,” for “negative numbers,” in BODMAS. So, do you deal with the negative sign before or after you handle the exponent? If you handle it first, then you’d raise -2 to the fourth power, which would give you an answer of 16. But if you hold off on it, you’d raise 2 to the fourth power, then make the answer negative, which would give an answer of -16.Here’s how to decide: a negative sign is the same thing as multiplying a number by -1. When you’re simplifying an expression, you handle the negative sign at the same time as you’d handle multiplication. That means it comes after the exponent, since M comes after E in the acronym. The right thing to do here is to raise 2 to the 4th power, then make the answer negative. The correct answer is -16.
You might also see negative numbers in Brackets: (-2)^4.Brackets come before exponents, so you handle the “multiplication” first. Then you raise -2 to the 4th power. The answer to this one is positive 16.
BODMAS and Fractions
Eg-
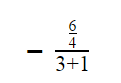
To simplify a complex fraction, you should pretend that there are three sets of invisible brackets: a set around the top of the fraction, another set around the bottom of the fraction, and finally, a third set around the entire thing.
Here’s how this fraction really looks:

Now apply BODMAS. Simplify everything inside each set of bracket as much as you can. Note that it’s fine to leave the numerator as an improper fraction.
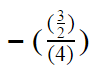
Now, divide 3/2 by 4, since that’s inside the outer set of bracket:

Put it all together. Here’s an expression that contains fractions, exponents, and negative numbers. Try simplifying it using BODMAS.

Don’t get intimidated by the multi-decker fraction. Find the longest, boldest line first, and split the fraction there:

Then simplify what’s in the brackets as much as you can. Work on the numerator first and be careful with the negatives:

Next, the denominator:

Here’s what the original fraction really says:

The whole thing simplifies to -1.
BODMAS and Equations
If you’re solving an equation like this one:
3x — 7 = 20
Add 7 to both sides. Next, divide both sides by 3. Addition first, then division. But BODMAS tells you to always divide before you add, right? Here’s why this happens.
Equations and expressions aren’t exactly the same thing. (-2)4 is an expression, and so is x³/x². On the other hand, 3x-7=20 is an equation. Remember this mnemonic: an equation contains an equals sign. BODMAS can be useful when you solve equations, but it’s really meant for expressions. When you’re simplifying an expression, BODMAS is a hard-and-fast rule. When you’re solving equations, you might do things in a different order, and that’s fine—as long as you understand the simplification you’re doing at each step.
2+3+3*11 bodmas rule
simplification problems using bodmas
bodmas questions and answers pdf
bodmas examples
bodmas questions test
bodmas exercises
bodmas rule pdf
bodmas questions for bank exams
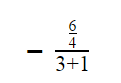 To simplify a complex fraction, you should pretend that there are three sets of invisible brackets: a set around the top of the fraction, another set around the bottom of the fraction, and finally, a third set around the entire thing.
Here’s how this fraction really looks:
To simplify a complex fraction, you should pretend that there are three sets of invisible brackets: a set around the top of the fraction, another set around the bottom of the fraction, and finally, a third set around the entire thing.
Here’s how this fraction really looks:
 Now apply BODMAS. Simplify everything inside each set of bracket as much as you can. Note that it’s fine to leave the numerator as an improper fraction.
Now apply BODMAS. Simplify everything inside each set of bracket as much as you can. Note that it’s fine to leave the numerator as an improper fraction.
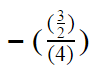 Now, divide 3/2 by 4, since that’s inside the outer set of bracket:
Now, divide 3/2 by 4, since that’s inside the outer set of bracket:
 Put it all together. Here’s an expression that contains fractions, exponents, and negative numbers. Try simplifying it using BODMAS.
Put it all together. Here’s an expression that contains fractions, exponents, and negative numbers. Try simplifying it using BODMAS.
 Don’t get intimidated by the multi-decker fraction. Find the longest, boldest line first, and split the fraction there:
Don’t get intimidated by the multi-decker fraction. Find the longest, boldest line first, and split the fraction there:
 Then simplify what’s in the brackets as much as you can. Work on the numerator first and be careful with the negatives:
Then simplify what’s in the brackets as much as you can. Work on the numerator first and be careful with the negatives:
 Next, the denominator:
Next, the denominator:
 Here’s what the original fraction really says:
Here’s what the original fraction really says:
 The whole thing simplifies to -1.
BODMAS and Equations
If you’re solving an equation like this one:
3x — 7 = 20
Add 7 to both sides. Next, divide both sides by 3. Addition first, then division. But BODMAS tells you to always divide before you add, right? Here’s why this happens.
Equations and expressions aren’t exactly the same thing. (-2)4 is an expression, and so is x³/x². On the other hand, 3x-7=20 is an equation. Remember this mnemonic: an equation contains an equals sign. BODMAS can be useful when you solve equations, but it’s really meant for expressions. When you’re simplifying an expression, BODMAS is a hard-and-fast rule. When you’re solving equations, you might do things in a different order, and that’s fine—as long as you understand the simplification you’re doing at each step.
2+3+3*11 bodmas rule
simplification problems using bodmas
bodmas questions and answers pdf
bodmas examples
bodmas questions test
bodmas exercises
bodmas rule pdf
bodmas questions for bank exams
The whole thing simplifies to -1.
BODMAS and Equations
If you’re solving an equation like this one:
3x — 7 = 20
Add 7 to both sides. Next, divide both sides by 3. Addition first, then division. But BODMAS tells you to always divide before you add, right? Here’s why this happens.
Equations and expressions aren’t exactly the same thing. (-2)4 is an expression, and so is x³/x². On the other hand, 3x-7=20 is an equation. Remember this mnemonic: an equation contains an equals sign. BODMAS can be useful when you solve equations, but it’s really meant for expressions. When you’re simplifying an expression, BODMAS is a hard-and-fast rule. When you’re solving equations, you might do things in a different order, and that’s fine—as long as you understand the simplification you’re doing at each step.
2+3+3*11 bodmas rule
simplification problems using bodmas
bodmas questions and answers pdf
bodmas examples
bodmas questions test
bodmas exercises
bodmas rule pdf
bodmas questions for bank exams
