- Question
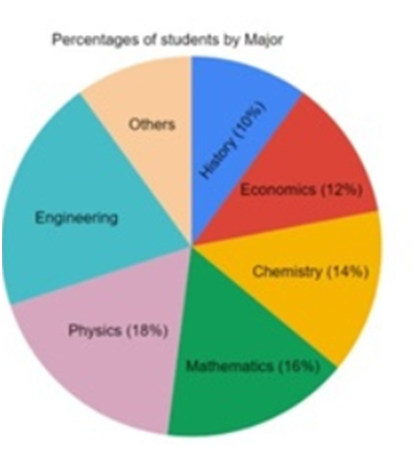
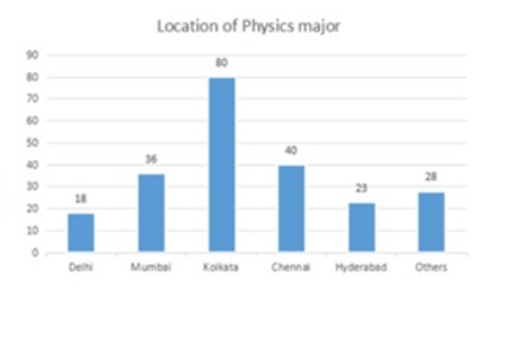
The break-up of the students in an University by subject major is given in the Pie-chart. The Bar Chart shows the number of students who major in Physics by geographic location.
If the proportion of Physics majors who are from Delhi is the same as the proportion of Engineering majors who are from Delhi, then determine, how many Engineering majors are there from Delhi ?
a)20
b)18
c)24
d)22
e)28
Explanation
SOLUTION[A] 20
Total number of Physics major from all locations = 225
… Total number of students = 225 0.18 = 1250
Number of engineering students = 20% * 1250 = 250
So, basis the given condition we have
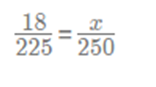
=> x = 20
Hence, option D
(Note: This question has been presented as was in the actual paper and has been solved by the aid of visual inference)
Question-2
Determine the number of students who major in Chemistry
a)190
b)180
c)200
d)170
e)175
Explanation
SOLUTION[175] E
Total number of Physics major from all locations = 225
… Total number of students = 225/0.18=1250
Number of students majoring in chemistry = 14% * 1250 = 175
Hence, option E
Question-3
12 percent of all students are from Chennai. What is the largest possible percentage of Economics students (rounded off to the nearest integer) that can be from Chennai ?
a)12
b)68
c)70
d)73
e)77
Explanation
SOLUTION[D] 73
Total number of Physics major from all locations = 225
… Total number of students = 225/0.18=1250
Students from Chennai = 12% * 1250 = 150
Given, number of Physics majors from chennai = 40
… maximum possible number of economic students from chennai = 150-40 = 110
Maximum percentage of students = 110/150*100%=73.33%
Hence, option D
Question – 4
Read the information provided below and answer the questions that follow :
Simple Happiness index (SHI) of a country is computed on the basis of three parameters:
Social Support (S),
Freedom to Life choices (F) and
Corruption Perception (C).
Each of these three parameters is measured on a scale of 0 to 8 (integers only). A country is then categorized based on the total score obtained by summing the scores of all the three parameters, as shown in the following table:
| Total score | 0-4 | 5-8 | 9-13 | 14-19 | 20-24 |
| Category | Very unhappy | unhappy | neutral | happy | Very happy |
Following diagram depicts the frequency distribution of the scores in S, F and C of 10 countries – Amda, Benga, Calla, Delma, Eppa, Varsa, Wanna, Xanda, Yanga and Zooma:
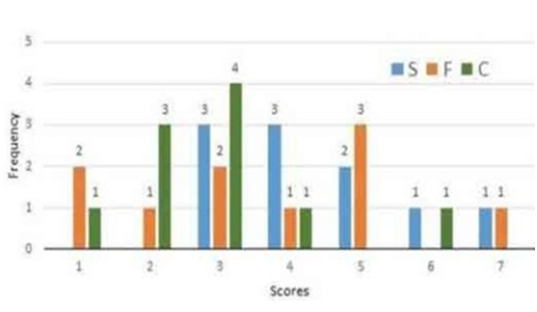
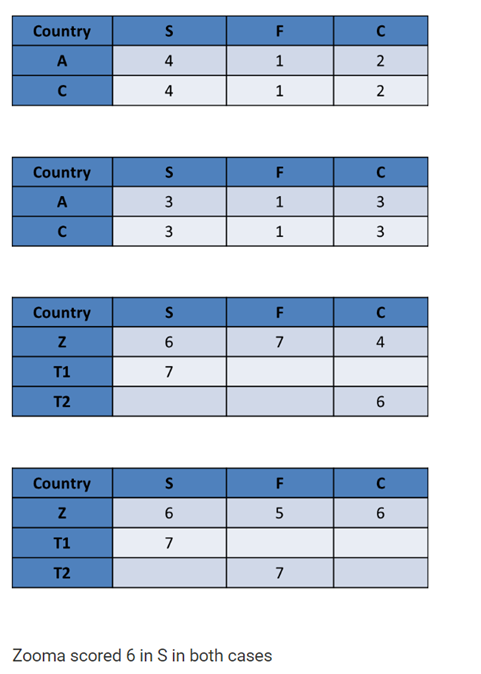
Further, the following is known:
1.Amda and Calla jointly have the lowest total score, 7, with identical scores in all the three parameters.
2.Zooma has a total score of 17.
3.All the 3 countries, which categorised as happy, have the highest score in exactly one parameter.
Benga and Delma, two countries categorized as happy, are tied with the same total score.
What is the maximum score they can achieve?
a)13
b)17
c)15
d)17
e)16
Explanation
SOLUTION[C]
15
Question-5
What is zooma score in S ?
a)3
b)6
c)7
d)8
e)5
Explanation
SOLUTION[B] 6
Some simple inferences
1. No one has got any 8 or 0.
2. Score of 3 is the most frequent, scores of 4 and 5 come right after that
Now, let us look at some of the constraints
Total adding up to 7 – this can be {1, 1, 5), (1, 2, 4), (1, 3, 3), (2, 2, 3} in some
order.
A and C get identical scores. So, if one gets {1, 1, 5), the other also should have got {1, 1, 5}.
We do not even have four 1’s, so {1, 1, 5} is ruled out.
We have 1 two from F, and 3 twos from C. So, we cannot have {2, 2, 3} either.
Both A and C could have got a 2 with C, but they both could not have gotten a
score of 2 with F.
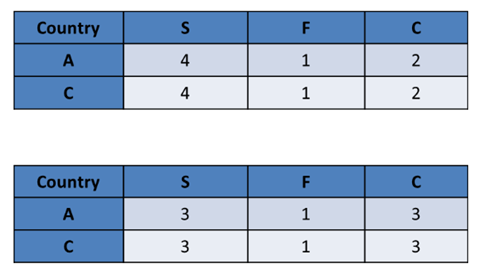
Both {1, 2, 4} and {1, 3, 3} are possible.
Only F = 1 is possible. Only C = 2 is possible. So, more specifically, we have two possibilities
Total adding up to 17 – this can be {7, 6, 4}, {7, 5, 5} or {6, 6, 5} in some order.
Z cannot be (7, 5, 5}.
Why not? Think about this
Only S and F have scores of 7 and 5. There is no C score or 7 or 5. So, Z has to
be either (7, 6, 4} or {6, 6, 5}.
Z has to be either {7, 6, 4} or {6, 6, 5). One Country should have scored highest in S, one in F and one in C. All three totals add up to 14 or more.
Let us call the three as happy Countries as Z, T1, T2 and build possible scenarios.
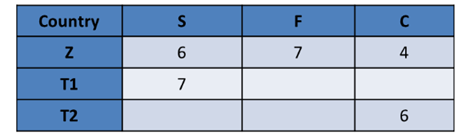
Let us start with Z = \{7, 6, 4\} In this case, Z should have scored the highest in S or F. So some other Country should have scored the highest in C. So, some other Country gets C = 6, Z should get S = 6 So, Z should have got F = 7
Let us start with Z = \{7, 6, 4\} In this case, Z should have scored the highest in S or F. So some other Country should have scored the highest in C. So, some other Country gets C = 6, Z should get S = 6 So, Z should have got F = 7. T1 should have S = 7 and T2 should have C = 6
Alternatively Z = \{6, 6, 5\} In this case, Z should have scored the highest in C. So
the other two Countries should have scored the highest in S and F. Both these Tables appear possible.
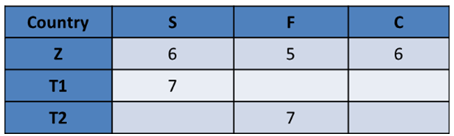
Incorporating all possibilities