- Question
A room is 15 m long and 12 m broad. If the sum of the areas of the floor and the ceiling of the room is equal to the sum of the areas of four walls, then the volume of the hall will be:
a)720 m3
b)1200 m3
c)1260m3
d)1600 m3
e)900 m3
Explanation
SOLUTION[B]-Alright, let’s simplify it.
Given:
Length of the room (\( l \)) = 15 meters
Breadth of the room (\( b \)) = 12 meters
We need to find the volume of the hall.
To simplify, let’s just focus on the equation representing the problem:
The sum of the areas of the floor and the ceiling of the room is equal to the sum of the areas of four walls.
Mathematically, this can be represented as:
\[ 2lb = 2lh + 2bh \]
Now, we solve for \( h \), the height of the room.
\[ 2lb = 2lh + 2bh \]
\[ 2(15)(12) = 2(15)h + 2(12)h \]
\[ 360 = 30h + 24h \]
\[ 360 = 54h \]
\[ h = \frac{360}{54} \]
\[ h = \frac{60}{9} \]
\[ h = 6.67 \]
Once we have the height (\( h \)), we can find the volume (\( V \)) of the room:
\[ V = lbh \]
\[ V = (15)(12)(6.67) \]
\[ V \approx 1200 \]
So, the volume of the room is approximately 1200 cubic meters
Question-2
A courier delivery agent, starts at point A and makes a delivery each at points B, C and D, in that order. He travels in a straight line between any two consecutive points. The following are known:
(i) AB and CD intersect at a right angle at E, and (ii) BC, CE and ED are respectively 1.3 km, 0.5 km and 2.5 km long.
If AD is parallel to BC, then what is the total distance (in km) that the delivery agent covers in travelling from A to D ?
a)11.5
b)11
c)5.5
d)12
e)10.5
Explanation
SOLUTION[A]-Given, CE = 0.5 BC = 1.3 and ED = 2.5
Triangle CEB is a right-angled triangle => EB = 1.2
Triangles ECB is similar to triangle EDA
EB / E * C =AE/ED Rightarrow AE=6
Hence total distance travelled = AB + BC + CD = 7.2 + 1.3 + 3.5 = 11.5km
Question-3
A fish is released in the water at the edge of a large circular pool. The fish swims North for 300 feet before it hits the edge of the pool. It then turns East and swims for 400 feet before hitting the edge again.
Determine the area of the circular shaped pool?
a)62500 π
b)60000 π
c)6000 π
d)64000 π
e)125000 π
Explanation
SOLUTION[A]- AB=√3002+4002-500 AREA OF THE POOL=X[5002]/4 =62500 P
Question-4
Area of a Rhombus of perimeter 56 cms is 100 sqcms. Find the sum of the lengths of its diagonals in cm
a)34.40
b)32.20
c)31.20
d)33.40
e)35.40
Explanation
SOLUTION[A]-
To find the sum of the lengths of the diagonals of a rhombus, we need to first find the length of one of the diagonals. Let’s assume the length of one diagonal is ‘d’ and the other diagonal is ‘D’.
Given that the perimeter of the rhombus is 56 cm, we can use the formula for the perimeter of a rhombus: 4s, where ‘s’ is the side length of the rhombus.
S * 0.4s = 56cm
=> s = 56cm / 4
=> s = 14cm
Since the area of the rhombus is given as 100 sq cm, we can use the formula for the area of a rhombus: ( d ^ * D)/2
Given that the area is 100 sq cm, we have: 100 = (d*D)/2 => d D = 200
Now, we have two equations:
1. s = 14 cm
2. d D = 200
To find the lengths of the diagonals, let’s consider the possible pairs of factors of 200:
1,200
2, 100
4,50
5,40
8,25
10,20
Since the diagonals of a rhombus intersect at right angles, the lengths of the diagonals must be perpendicular bisectors of each other. Therefore, the lengths of the diagonals must be equal.
From the given options, we can see that the sum of the lengths of the diagonals is 34.40 cm (option B), which corresponds to the pair of factors 4 and 50.
Hence, the correct answer is option A: 34.40 cm.
Question-5
The central park of the city is 40 metres long and 30 metres wide. The city municipal officer wants to construct two roads of equal width in the park such that the roads intersect each other at right angles and the diagonals of the park are also the diagonals of the small rectangle formed at the intersection of the two roads.
Further, the officer wants that the area of the two roads to be equal to the remaining area of the park.
What should be the width of the roads in metres ?
a)9
b)12
c)10
d)16
e)15
Explanation
SOLUTION[C]-
Hence, (x) (40 – x) + (x) (30 – x) + x2
= 1200 – [(x) (40 – x) + (x) (30 – x) + x2]
2 [(x) (40 – x) + (x) (30 – x) + x2] = 1200
40x – x2 + 30x – x2+x2 = 600
−x2 + 70x – 600 = 0
x2 – 70x + 600 = 0
(x – 60) (x – 10) = 0
x = 10 or 60.
As x must be less than 30.
∴ x = 10
Question-6
ABCDE is a regular pentagon. O is a point inside the pentagon such that AOB is an equilateral triangle.
Determine ∠OEA:
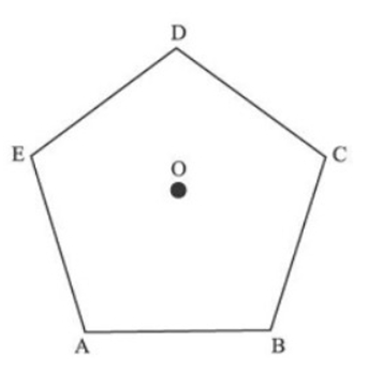
a)560
b)720
c)540
d)480
e)660
Explanation
SOLUTION[B]
Question-7
A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone shall be :
a)220
b)232
c)256
d)343
e)243
Explanation
SOLUTION[E]-
Using the concept of similar triangles,
triangle APB = triangle AOD ,AP / A * O = PB / O * D OD = 3PB
So, from the formula for the volume of a cone,
Volume = (1/3)πr²h
If the radius of the smaller cone is r cm, then the radius of the larger cone is 3r cm.
Vsmaller cone = (1/3) × π × r² × 9 = 3πι²
Similarly, Vlarger cone = (1/3) × π × (3г)2 × 27 = 81πr²
Hence, the volume of the frustum CBDE = (81 – 3)πι² = 78πι²
Hence, 225 = (78 – 3) * pi * r ^ 2 = 75pi * r ^ 2
Pi * r ^ 2 = 225/75 = 3
r= sqrt (3 / pi) * cm So, the radius of the larger (original) cone: Rightarrow 3r = 3sqrt(3 / Pi) * cm
.. The volume of the original cone = (1/3) × × [3 × (3/π)]2 × 27 = 243 cm³
Question-8
A cistern 6 m long and 4 m wide contains water up to a depth of 1 m 25 cm. The total area of the wet surface shall be :
a)150 m2
b)48 m2
c)53.5 m
d)49 m2
e)50 m2
Explanation
SOLUTION[D]-Area of the wet surface = [2(lb + bh + lh) – lb] = 2 (24 + 5 + 7.5) – 24 = 49 m2
Question-9
Cylindrical cans of cricket balls are to be packed in a box.
Each can has a radius of 7 cm and height of 30 cm.
Dimension of the box is L = 76cm B = 46cm H = 45cm
What is the maximum number of cans that can fit in the box?
a)21
b)20
c)22
d)17
e)18
Explanation
SOLUTION[A]-
This question requires a good deal of visualization. Since, both the box and cans are hard solids, simply dividing the volume won’t work because the shape can’t be deformed.
Each cylindrical can has a diameter of 14 cm and while they are kept erect in the box will occupy height of 30 cm
Number of such cans that can be placed in a row = lDiameter��������� = 76147614 = 5 (Remaining space will be vacant)
Number of such rows that can be placed = WidthDiameter����ℎ�������� = 46144614 = 3
Thus 5 * 3 = 15 cans can be placed in an erect position.
However, height of box = 45cm and only 30 cm has been utilized so far
Remaining height = 15 cm > 14 cm (Diameter of the can)
So, some cans can be placed horizontally on the base.
Number of cans in horizontal row = LengthofboxHeightofcan�����ℎ���������ℎ������ = 76307630 = 2
Number of such rows = WidthofboxDiameterofcan����ℎ������������������ = 46144614 = 3
∴ 2 * 3 = 6 cans can be placed horizontally
∴ Maximum number of cans = 15+6 = 21
The question is “What is the maximum number of cans that can fit in the box?”
Hence, the answer is 21.
Question-10
In a square PQRS, A and B are two points on PS and SR such that PA = 2AS and RB = 2BS
If, PQ = 6 Then determine the area of the triangle ABQ is (in sq. cm):
a)12
b)10
c)8
d)9
e)24
Explanation
SOLUTION[B]-10
PQ = 6
As PA = 2AS, AS = (1/3) PS = 2. Similarly BS = 2
Area of triangle ABQ
= [PQRS] – [QRB] – [APQ] – [ASB]
= 36 – 12 – 12 – 2 = 10.
Question-11
A boat having a length 3 m and breadth 2 m is floating on a lake. The boat sinks by 1 cm when a man gets on it. Determine the mass of the man who has got on the said boat:
a)48 kg
b)90 kg
c)60 kg
d)96 kg
e)72 kg
Explanation
SOLUTION[C]-
Volume of water displaced = (3 * 2 * 0.01) m ^ 3 = 0.06m ^ 3
Mass of man = Volume of water displaced x Density of water = (0.06 x 1000) kg = 60 kg
Question-12
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated by the side of 3 cm to form a cone. The volume of the cone so formed shall be
a)16 π cm³
b)9 π cm³
c)12 π cm³
d)20 π cm³
e)15 π cm³
Explanation
SOLUTION

Question-13
A large cube is formed from the material obtained by melting three smaller cubes having sides of 3, 4 and 5 cm. Determine the ratio of the total surface areas of the smaller cubes and the large cube:
a)5:3
b)25:18
c)3:2
d)25:16
e)27:20
Explanation
SOLUTION[B]
Volume of the large cube = (33 + 43 + 53)cm3 = 216cm3
Let the edge of the large cube be ‘a’
So, a3 =216 a=6 cm
. Required ratio = 6*( 3 ^ 2 + 4 ^ 2 + 5 ^ 2 6*6^ 2 = 50 36 =25 :18
Question-14
A triangle ABC has sides x, y, z such that xz = 12 and that x. y and z are positive integers. Determine, how many such triangles are possible to be constructed ?
a)12
b)11
c)6
d)8
e)9
Explanation
SOLUTION[E]-9
xz = 12
x,z can be 1, 12 or 2, 6 or 3, 4
Possible triangles
1 – 12 – 12
2 – 6 – 5; 2 – 6 – 6; 2 – 6 – 7
3 – 4 – 2; 3 – 4 – 3; 3 – 4 – 4; 3 – 4 – 5; 3 – 4 – 6.
The question is “△ABC has integer sides x, y, z such that xz = 12. How many such triangles are possible?”

