In a hockey tournament, total of 500 points were scored by 7 players in two matches together. The total
points scored in the first match was 50% more than that of the second match. The pie chart 1 and pie chart 2
gives the information about the percentage breakup of the points scored in the first match in the second
match respectively
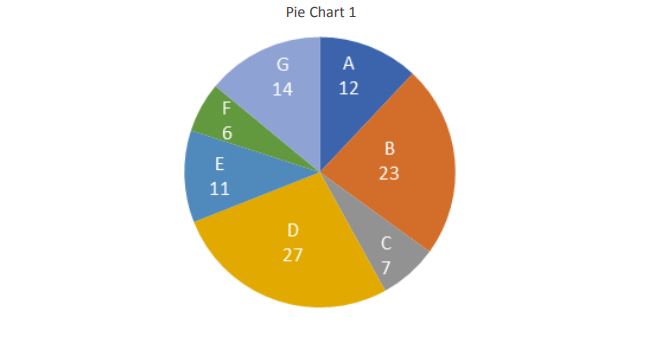
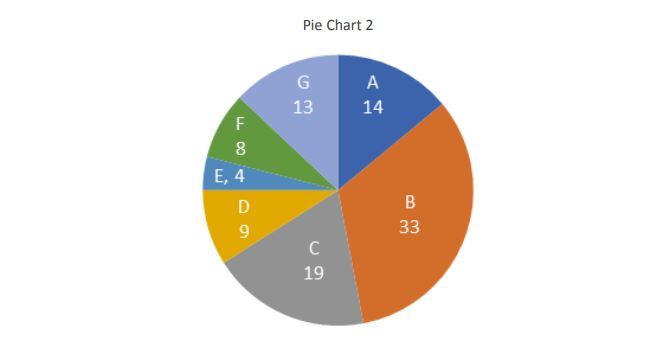
1. Which of the following players had scored the least number of points in the two
matches together?
A. F
B. E
C. A
D. G
E. C
2. The total points scored by B in the both matches together was what percent of the
total points of both the matches together?
A. 37%
B. 33%
C. 29%
D. 27%
E. None of these
3. In the tournament, the highest number of points scored by any player was how many
more than that of lowest number of points scored by any player?
A. 99
B. 103
C. 101
D. 107
E. None of these
4. What is the ratio between the total number of points scored by the player A and that
by the player G in the both matches together?
A. 32 : 33
B. 32 : 31
C. 16 : 19
D. 16 : 17
E. None of these
5. The number of points scored by A and B together in the first match was how much
more than that by F and G together in the second match?
A. 45
B. 65
C. 66
D. 63
E. None of these
Explanation
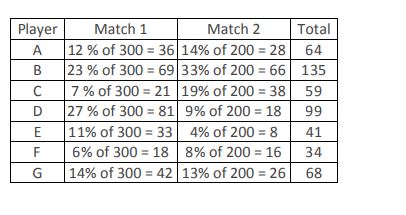
Question 1-
Following the common explanation, we get
Let in the match 2, the total points scored = 2x then in the match 1, the total point scored = 150% of 2x
= 3x
2x + 3x = 500
x = 100
In match1, the total points scored = 300 and in the match2, the total points scored = 200
The least number of points scored by the player F = 34
Hence, option A is correct.
Question 2-
Following the common explanation, we get
The total number of points scored by B in the both match together = 135
The reqd. % = 135 × 100/500 = 27%
Hence, option D is correct.
Question 3-
Following the common explanation, we get
The highest number of points scored by the player B = 135
The lowest number of points scored by the player F = 34
The required difference = 135 – 34 = 101
Hence, option C is correct.
Question 4-
Following the common explanation, we get
The total number of points scored by the player A = 64
The total number of points scored by the player G = 68
The required ratio = 64 : 68 = 16 : 17
Hence, option D is correct
Question 5-
Following the common explanation, we get
The number of points scored by A and B together in the first match = 36 + 69 = 105
The number of points scored by F and G together in the second match = 16 + 26 = 42
The required difference = 105 – 42 = 63
Hence, option D is correct.

