Statements:
No toffee is coffee.
No sweet is toffee.
Conclusions:
I. No coffee is sweet.
II. All sweets are coffee.
A. if only conclusion I follows.
B. if only conclusion II follows.
C.if either conclusion I or conclusion II follows.
D.if neither conclusion I nor conclusion II follows.
E.if both conclusion I and conclusion II follow.
Explanation
ANS : D
Venn Diagram Method:

Analytical Method:
E + E = No conclusion
Thus, neither conclusion I nor conclusion II follows.
Hence, option D is correct.
Statements:
All windows are doors.
All entrances are windows.
No gate is a door.
Conclusions:
I. At least some windows are gates.
II. No gate is an entrance.
A.if only conclusion I follows.
B.if only conclusion II follows.
C.if either conclusion I or conclusion II follows.
D.if neither conclusion I nor conclusion II follows.
E.if both conclusion I and conclusion II follow
Explanation
ANS : B
Venn Diagram Method:
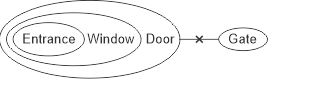
Analytical Method:
All entrances are windows (A) + All windows are doors (A) + [No gate is a door (E)] = No door is a gate (E) = A + E = E = No entrance is a gate.
Hence, conclusion II follows .
Again,
All window are doors (A) + [No gate is a door (E)] = No door is a gate (E) = A + E = E = No window is a gate.
Thus, conclusion I does not follow.
Hence, option B is correct.
Statements:
All bottles are glasses.
No cup is a glass.
Conclusions:
I. No bottle is a cup.
II. At least some glasses are bottles.
A.if only conclusion I follows.
B.if only conclusion II follows.
C.if either conclusion I or conclusion II follows.
D.if neither conclusion I nor conclusion II follows.
E.if both conclusion I and conclusion II follow.
Explanation
Venn Diagram Method:
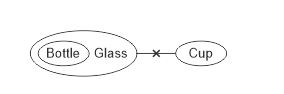
Analytical Method:
All bottles are glasses (A) + [No cup is a glass (E)] = No glass is a cup (E) = A + E = E = No bottle is a cup.
Hence, conclusion I follows.
Again,
All bottles are glasses (A) = Some glasses are bottles (I). It means,
At least some glasses are bottles.
Hence conclusion II follows.
Thus, both conclusion I and II follow.
Hence, option E is correct.
Statements :
All frocks are trousers.
No pants are frocks.
Some jackets are pants
Conclusions :
I. At least some jackets are frocks.
II. No jacket is a frock.
A.If only conclusion I follows.
B.If only conclusion II follows.
C.If neither conclusion I nor II follows.
D.If both conclusion I and II follows.
E.If either conclusion I or II follows.
Explanation
ANS : E
Checking C1: At least some jackets are frocks.
Using S3 and S2,
Some jackets are pants + No pants are frocks = Some jackets are not frocks. Hence, C1 doesn’t follow.
Checking C2: No jacket is a frock.
Clearly, we can observe that we have already got a definite conclusion above between the classes ‘jacket’ and ‘frock’. Hence, C2 doesn’t follow either.
However, we closely observe, we can find that both C1 and C2 together form a complementary pair and therefore either C1 or C2 definitely follows.
Option E is hence the correct answer.
Statements :
All bottles are jugs.
All pans are jugs.
Some jugs are not mugs.
Conclusions :
I. Some bottles are not pans.
II. Some mugs may not be jugs.
A.If only conclusion I follow
B.If only conclusion II follow
C.If neither conclusion I nor conclusion II follows
D.If both the conclusions follow
E.If either conclusion I or conclusion II follows.
Explanation
ANS : B
Checking Conclusion I: Some bottles are not pans.
Here, neither S1 nor S2 is a negative statement, a negative conclusion between the classes of ‘Bottles’ and ‘Pans’ is not possible. C1, hence, doesn’t follow.
Checking Conclusion II: Some mugs may not be jugs.
In S3 it’s given that ‘Some jugs are not mugs’. Here, we are not sure of the elements of the class ‘Mugs’. Clearly, we can say that ‘Some mugs may not be jugs’. C2, hence, follows.
Option B is hence the correct answer.

